

We are living in a period of such overwhelming acceptance of the Cartesian system of co-ordinates, based on three axes in 90 degree co-ordination, that it might be considered intellectual suicide, or at least a risky and eccentric affair, to speak of an alternative system of co-ordinates and to maintain, that such a different system would have considerable advantages over what is now generally accepted. Yet, an alternative system has been discovered and is available for refinement and use.
Ren'e Descartes, whose birth date we celebrate this year as having occurred exactly four centuries ago, has made prodigious contributions to science and philosophy, introducing reasoning where authority had been the dominating factor before his time. We will concern ourselves here with only one of his many feats, the introduction of a rational system of co-ordinates, with which to locate the precise position of any object inside a known space.
According to anecdote, Descartes invented the presently used system of co-ordinates observing and contemplating the erratic course of a fly in his room and realizing that, if he could determine the distance to each one of the three "axes" formed by one of the rectangular corners of the room, he could be sure of its exact position, and that a succession of such co-ordinates would define the otherwise elusive curves that marked the fly's course. Although we cannot be sure that this anecdote correctly survived the centuries, it seems reasonable to assume that the Cartesian system of co-ordinates was in fact based on the geometry of construction that is prevalent until this day, that is, a rectangular configuration of most houses and of the rooms inside.
R. Buckminster Fuller, on the other hand, lived somewhat closer to present time than Descartes; he died in 1983 at the age of 87. Like Descartes, Fuller has made copious contributions to science and philosophy. He is probably best known for his invention of the geodesic dome, a structure of triangularly-interconnected elements that has the best ratio of weight to enclosed space of any artificial construction so far developed. More recently, Fuller has received much public acclaim for having predicted, with his geometry, the existence of spherical molecules. The experimental discovery of the Buckminsterfullerene, a spherical and extraordinarily stable large molecule of carbon, is only a few years old.
Fuller's geometry goes by the name of Synergetics and has been developed by experimentally observing the behavior of spheres of equal diameter, when packed as close as possible to form regular geometric figures. The basic and most simple stable geometric configuration of synergetic geometry is the tetrahedron, formed by four spheres laying next to each other, in perfect triangular configuration forming four angles of 60 degrees (fig. 1). Other important elements are the octahedron (formed by six closest-packed spheres) and the vector equilibrium, which is the result of twelve spheres nested around a thirteenth, central sphere, in omnidirectional closest-packing, 60 degree co-ordinated configuration.
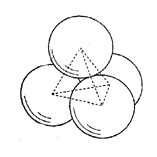
Fig.1
The cube, which is at the basis of our present-day construction methods and of the x-y-z Cartesian co-ordinate system, is not in and by itself a stable configuration. Eight spheres forming a cube are inherently unstable. To gain stability, they must be artificially stabilized by interconnecting them in the way the tetrahedron is connected. In this way, two tetrahedra of four spheres each, joined at their respective centers, form one cube of eight spheres.
It happens that this geometry, as developed by Fuller, is in perfect accord with how crystals grow in their various forms, and that its application in engineering reveals to us the possibility of very efficient structures in terms of economy of raw materials and strength of the resulting construction.
Now how could the discoveries of Fuller be utilized to form a co-ordinate system and why should we venture to do such a task, seeing that the Cartesian x-y-z co-ordinates have done perfect (or almost perfect) service for such a long time?
For one, Cartesian co-ordinates may be a convenient mathematical construct, but they do not accord with nature's ways any more than modern chemistry will ever be able to duplicate the conditions of living organisms.
If we utilize x-y-z co-ordinates not for orientation in a known enclosed space (such as did Descartes), but in space with unknown extension, if our system of three axes in other words does not form one of the corners of a known space, but the point of origin of space extending in all directions, the original three axes are no longer sufficient for orientation. We must double the system, adding a mirror image of the three axes, to be able to describe the space 'on the other side of the corner' (fig. 2).
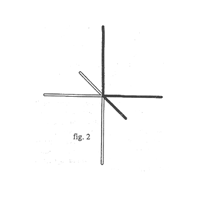
Normally we do not think of this action as a doubling of the axes, as we simply assign negative values to one of the sides, and positive values to the other. But rigorously, we now have six axes: plus x and minus x, plus y and minus y, as well as plus z and minus z. The fact that the plus and minus parts of each axis seem like one continuous axis does not justify considering them to be one. In fact, for the purpose of orientation, we must specify whether we are locating something on the plus axis or on the minus axis, even if we chose to do so by considering positive numbers to belong to the plus axis and negative ones to the minus axis. So we have, in actual fact, six axes to consider and in order to locate an object in space, we must define its position in relation to three out of six axes.
This is where Fuller's synergetic geometry suggests a way of simplifying our task enormously. If we decide to reduce the number of axes from six to four, taking the basic and most simple stable geometric figure, the tetrahedron, as our point of reference, we may locate any point in space by defining its position with regard to three out of four (not three out of six!) axes of reference. The four axes of reference in this system of co-ordinates are the axes that originate at each one of the vertices of the tetrahedron, intersecting at its midpoint and passing through the middle of each one of the triangles opposite these vertexes (fig. 3). These axes are co-ordinated with angles of 120 degrees. The four of them represent the minimum set of reference axes emanating from a common origin needed for defining all possible directions in physical space.
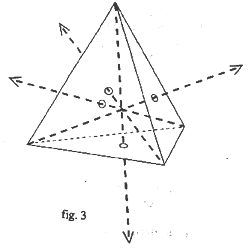
CMYK (cyan-magenta-yellow-black) are the four colours used by present day printing presses. The combination of these four colours in various percentages creates a large number of different colours in almost endless continuous shading. Assigning one of the basic colours to each one of the four axes of the tetrahedron, and blending them towards the other axes, we obtain in fact a unique colour for each one of the thousands or millions of possible directions that we may want to instantly identify. Naturally we can also express direction in terms of degrees, minutes and seconds of arc in relation to the three nearest axes.
In the printed version of the article, a tetrahedron is supplied which
can be cut out and pasted
together, to illustrate the principle of color coding.
A co-ordinate system of this kind, suitably developed and refined, may be used with profit in astronomy, in navigation (especially space navigation), in holographic representation of images, in crystal-based electronic information storage and possibly a whole range of other, yet-to-be-thought-of activities.
By its use, we transform our four directions of orientation on earth (east-west-north-south) into four directions of orientation in space. We need to develop and use this tool if we are seriously considering to expand our influence into planetary or interstellar space, not only in the sense of observation, but also of exploration and navigation.
One last comment on the concept of 'dimension', which seems to be not very well understood by current scientific inquiry.
We are accustomed to calling this physical universe a three-dimensional universe. Text books and encyclopedias tell us that space has three dimensions, without considering that the number of dimensions we assign to space depends only on the kind of geometric reference we are using. I was tempted to say, in a first moment, that considering tetrahedric space co-ordinates, obviously space must have four dimensions. But that would be making the same mistake as our current authoritative teachings.
Space in fact has only one 'dimension' which we may also call 'extension'. It extends equally into all directions. It does not matter how many directions we choose to refer to in our systems of orientation, three, four, six, maybe ten. We are still considering the same space. The term three-dimensional has as little physical relevance as would the term four-dimensional or n-dimensional. Dimensions, after all, are only a conceptional tool of convenience for expressing in mathematical terms a particular way of looking at or of trying to comprehend the reality of what we call space.
Josef Hasslberger
3 February 1996
References:
1. Fuller, R. Buckminster "Synergetics", 1982, Macmillan Publishing
Company,
866 Third Avenue, New York, N.Y. 10022
2. Fuller, R. Buckminster"Cosmography", 1991, Macmillan Publishing Company
For more information about Buckminster Fuller and his work, contact:
Buckminster Fuller Institute, 1743 South La Cienega Blvd., Los Angeles,
CA 90035
Telephone (213) 837 7710
Three interesting pages on the web about Fuller and about tetrahedric
space geometry:
http://www.teleport.com/~pdx4d/synhome.html
http://www.teleport.com/~pdx4d/quadrays.html
http://www.teleport.com/~pdx4d/quadcolors.html